P14576 Lamborghini (Remix)

发表于 更新于

P14576 Lamborghini (Remix)

题目描述

光标是一种可以出现在一行代码的相邻两个字符之间，或者某行代码末尾，或者某行代码开头的标识。

在现代的代码编辑器中，我们通常可以同时放置许多光标。

当按下左方向键时，所有光标都会各自同时向左移动一个字符。特别地，在当前行开头的移动至上一行末尾，在第一行开头的光标消失。

当按下右方向键时，所有光标都会各自同时向右移动一个字符。特别地，在当前行末尾的移动至下一行开头，在最后一行末尾的光标消失。

现在张均好有一份 $n$ 行的代码，第 $i$ 行代码的长度为 $a_i$（即一个长度为 $a_i$ 的字符串）。张均好想知道，如果他选择一些行的末尾放置光标，再通过若干次按方向键，最多能使同一行包含多少个光标，注意某一行的开头和末尾也属于这一行。

你只需输出这个最大值。

输入格式

本题包含多组测试。

每个测试点第一行一个整数 $T$，表示测试数据组数。

对于每组测试数据：

第一行一个整数 $n$，表示代码行数。

接下来一行 $n$ 个用空格隔开的整数，表示第 $i$ 行的代码长度为 $a_i$。

输出格式

对于每组测试数据，输出一行一个整数，表示答案。

输入输出样例 #1

输入 #1

1
2
3
4
5
6
7
3
7
24 20 20 12 6 6 22
10
10 7 2 3 5 6 4 13 21 30
5
2 3 4 5 6

输出 #1

1
2
3
3
6
2

说明/提示

样例 1 解释

这个样例描述了如下的代码：

1
2
3
4
5
6
7
#include <bits/stdc++.h>
#define ll long long
using namespace std;
int pi=3.14;
int a;
int b;
#define ld long double

显然，每行代码的长度分别为 $24,20,20,12,6,6,22$。

张均好可以在第 $4,5,6$ 行末尾放置光标：

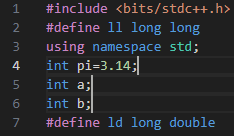
通过不断按下左方向键，这三个光标可以同时出现在第二行：

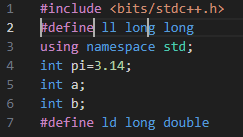
也可以通过不断按下右方向键，使得这三个光标同时出现在第七行：

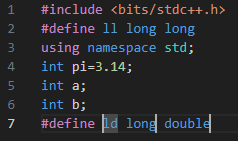
可以证明，不存在使得更多光标出现在同一行的方案。

数据范围

对于 $100\%$ 的数据，$1\le T\le 10$，$1\le n\le 2\times 10^5$，$1\le a_i\le 10^9$。

子任务 $n\le$ 特殊性质 分数
Subtask 1 $20$ 无 $20$
Subtask 2 $200$ 无 $20$
Subtask 3 $5000$ 无 $20$
Subtask 4 $2\times 10^4$ $a_i\le 1000$ $20$
Subtask 5 $2\times 10^5$ 无 $20$

思路分析 + 代码实现

我们希望有尽可能多的光标同时出现在一行内，那么这一行需要尽量长，所以我们找最长的一行作为我们最后放置这些光标的位置。现在的问题是，在这一行最多能同时放下几个光标呢？

我们定义两个光标的距离为一个光标到另一个光标所在位置所需要的最少移动次数。显然，同时移动所有光标是不会改变两个光标之间的距离的。在这种情况下，不难发现在长度为 $a$ 的一行中能放下 $n$ 个光标的必要条件是第 $1$ 个光标到第 $n$ 个光标的距离不大于 $a$。

同时我们发现，第 $i$ 行与第 $i+1$ 行的行末光标的距离为 $1+a_{i+1}$ （因为换一行需要一次移动）。所以，如果第 $i-1$ 行和第 $i+1$ 行的行末光标都能放入最长的那一行，那么第 $i$ 行的自然也行，即我们统计的答案中的光标初始时是在一段连续的行末的。

这样，问题就转化为了，对于 $a_{max}$ ，找出最大的一段连续的行末光标，使得第 $1$ 个光标到第 $n$ 个光标的距离不大于 $a$ ，此时的 $n$ 就是答案。可以用前缀和 + 双指针法实现，时间复杂度为 $O(nT)$ ，代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
constexpr LL MAXN = 2e5 + 1;
LL a[MAXN], b[MAXN];
LL sum(LL l, LL r) { // a_l 不用计入
    return b[r] - b[l];
}
int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    LL T, ans, max_line, n;
    cin >> T;
    while (T--) {
        cin >> n;
        max_line = 0;
        ans = 1;
        for(LL i = 1; i <= n; i++) {
            cin >> a[i];
            b[i] = 1 + a[i] + b[i - 1]; // 每次换行会多 1
            max_line = max(max_line, a[i]);
        }
        LL l = 1, r = 1;
        while (r <= n) {
            while (l < r && sum(l, r) > max_line)
                l++;
            while (r <= n && sum(l, r) <= max_line)
                r++;
            ans = max(ans, r - l);
        }
        cout << ans << "\n";
    }
    return 0;
}